Pythonによるデータ処理18 ～ 1Dランダムウォーク2

前回に引き続きPythonによるランダムウォークのシミュレーションについて取り上げる。今回は、1Dランダムウォークの問題であるステップ(2n)ではじめて原点に戻る確率について考える。

atatat.hatenablog.com

1. はじめて中心に戻る理論確率
2. はじめて中心に戻るシミュレーション確率
3. まとめ

1. はじめて中心に戻る理論確率

今回はランダムウォークでの2nステップ目ではじめて中心0にいる確率を求める。理論式は複雑なので以下を参照する。

zakii.la.coocan.jp

2nステップ目で0になる確率f_2nは

$\displaystyle f_{2n}=\frac{1}{2n 2^{2n-2}} \binom{2n-2}{n-1} \,(n\geq 1)$

n=1から∞までの和が1に収束するため、1Dランダムウォークは必ず中心0に戻ることが数学的に得られる。

$\displaystyle \sum_{n=1}^{\infty} f_{2n}= 1$

上の式をSymPyを用いて以下のように数値計算してみる。

from sympy import *
init_printing(False)
var('n  k')
import numpy as np
import matplotlib.pyplot as plt

step=100
st_t=[]
prop_theo=[]
for i in np.arange(1,int(step/2)+1,1):
 p=(1/(2*n*2**(2*n-2))*factorial(2*n-2)/(factorial(n-1)*factorial(n-1))).subs(n,i).evalf()
 prop_theo.append(p)
 st_t.append(int(2*i))

cm_prop_theo=np.cumsum(prop_theo)
plt.plot(st_t,cm_prop_theo)
plt.ylim([0,1])
plt.title('Theoretical Calculation')
plt.ylabel('Cumulative probability')
plt.xlabel('Steps')

100ステップでだいたい0.9程度になっている。階乗の直接計算のリソースの関係でステップ数を増やすと時間がかかる。（Stirlingの近似など使うとよいかもしれない）

2. はじめて中心に戻るシミュレーション確率

前回のコードを継承し、1000000x100の+1,-1を含むランダム行列を用いる。前回は行列の各ステップでの部分和が0になる行数を確率としていたが、今回は部分和が0になった行をnp.deleteを用いて削除する。ステップが進むごとに行数が減っていき、乱数シミュレーションとしてはサンプル数が少なくなるという懸念があるが、理論計算と同じく100ステップまで計算すると同じような曲線が得られた。

num=1000000
step=100
prop_sim=[]
st_s=[]
a=np.random.random((num,step))
a[a>=0.5]=1
a[a<0.5]=-1

for i in np.arange(2,step+2,2):
 sa=np.sum(a[:,:i],axis=1)
 ind=np.where(sa==0)
 c=np.size(ind)
 a=np.delete(a,ind,0)
 prop_sim.append(c/num)
 st_s.append(i)
cm_prop_sim=np.cumsum(prop_sim)
plt.plot(st_s,cm_prop_sim)
plt.ylim([0,1])
plt.title('Numerical Simulation')
plt.ylabel('Cumulative probability')
plt.xlabel('Steps')

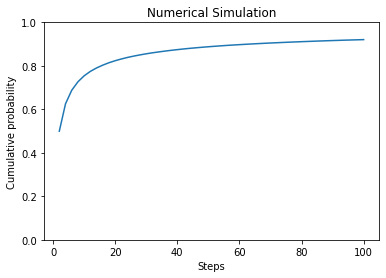
"はじめて0に戻るシミュレーション確率" — はじめて0に戻るシミュレーション確率

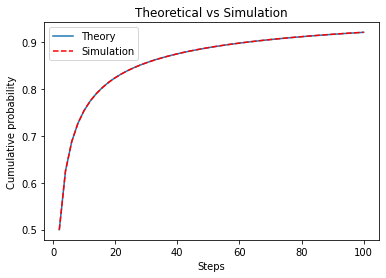
そこで、理論値と比較するとぴったり一致していた。

plt.plot(st_t,cm_prop_theo)
plt.plot(st_s,cm_prop_sim,'r--')
plt.title('Theoretical vs Simulation')
plt.ylabel('Cumulative probability')
plt.xlabel('Steps')
plt.legend(['Theory','Simulation'])