gnuplotによるグラフ作成36～sum演算子

　今回はgnuplotのsum演算子とその利用法としてフーリエ級数和のプロットと三角関数の無限積展開のプロットについて紹介しする。

1. sum演算子
2. 総乗演算への応用
3. まとめ

1. sum演算子

　sum演算子は和を計算する演算子で sim [i=開始:終了] 式という形で使用する。例えば1から10までの和は

print sum[i=1:10] i
>55.0

sum演算子を利用すれば多項式の和を表示することができる。なお再帰定義でも同じようなことができるが、反復回数が100回程度の制限されているが、sum演算子では時間がかかるものの100回以上の和をとることもできる。例えば多項式として以下のステップ関数のフーリエ級数和をsum演算子を用いてプロットすることができる。

$\displaystyle step(x)=\frac{2}{\pi}\sum_{n=1}^{\infty} ( 1-(-1)^{n} ) \frac{\sin (nx )}{n}$

step_f(x,n)=sum[i=1:n] 2/pi*(1-(-1)**i)*sin(i*x)/i
set samples 5000
plot step_f(x,10),step_f(x,100),step_f(x,500)

級数が大きくなるほどステップ関数に近づくことがわかる。同様にのこぎり波は以下のフーリエ級数であらわすことができ、そのフーリエ級数和をsum演算子を利用してプロットする。

$\displaystyle saw(x)=1 - \sum_{n=1}^{\infty} \frac{\sin (nx )}{n\pi}$

saw_f(x,n)=1+sum[i=1:n] -1/(i*pi)*sin(i*x) 
plot saw_f(x,10), saw_f(x,100),saw_f(x,500)

2. 総乗演算への応用

sum演算子は多項式の和だけでなく、利用して階乗を求めることもできる。以下のように３項演算子と組み合わせて評価したいループに達したらその値を返し、それ以外は0とする。

a=1
 print sum [i=1:5] (a=a*i, (i==5?a:0))
>120.0

応用例として正弦波の無限積展開

$\displaystyle \sin(x)=x \prod_{n=1}^{\infty} \left( 1-\frac{x^{2}}{ n^{2} \pi^{2} } \right)$

をsum演算子と3項演算子を用いて以下のようにプロットすることができる。初項(i=1)ならば初期値a=(1-(x/pi/i)2)を与え、それ以外は前項との積a=a*(1-(x/pi/i)2)をとるように3項演算子で記述する。2つめの3項演算子は指定のn以外は0になるように用いる。

p_sin(x,n) =x*sum[i=1:n] ((i==1 ? a=(1-(x/pi/i)**2) :a=a*(1-(x/pi/i)**2)),(i==n?a:0))  
set samples 1000
set xrange[-50:50]
 plot sin(x), p_sin(x,10),p_sin(x,100),p_sin(x,500)

nが大きくなるほど発散が抑えられてsin関数と一致する。

同様に双曲線関数 coshの無限積展開に適用する。

$\displaystyle \cosh(x)= \prod_{n=1}^{\infty} \left( 1-\frac{x^{2}}{ (n-1/2)^{2} \pi^{2} } \right)$

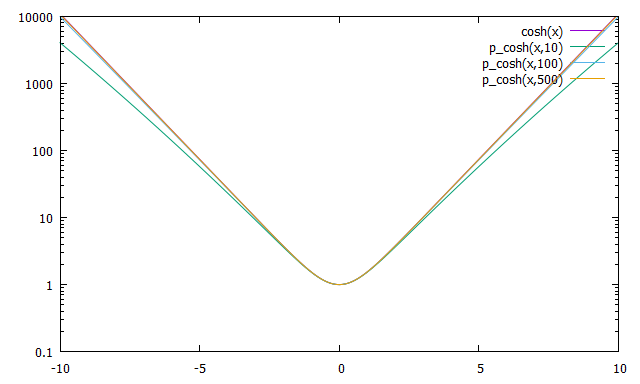
p_cosh(x,n) =sum[i=1:n] ((i==1 ? a=(1+(x/pi/(i-0.5))**2) :a=a*(1+(x/pi/(i-0.5))**2)),(i==n?a:0))
set xrange[-10]10]
set yrange[0:1000]
set logscale y
plot cosh(x),p_cosh(x,10),p_cosh(x,100),p_cosh(x,500)