今回はOpen CVのWatershedによる輪郭抽出について紹介したい。
1. Watershedによる輪郭抽出
Watershedによる輪郭抽出の利点としては、輪郭、境界同士が接している場合について輪郭・境界がつながることないという点にある。
OpenCVのWatershedアルゴリズムやコードの解説は以下にあるが、
Watershedアルゴリズムを使った画像の領域分割 — OpenCV-Python Tutorials 1 documentation
おおまかな処理の流れは、2値化→ノイズ処理、境界除去→マーカー作成→Watershed関数適用となる。
Watershedのチュートリアルではコイン画像に適用しているが、今回は以前輪郭抽出で使用した赤血球画像について適用してみる。
atatat.hatenablog.com
2値化画像を用いた輪郭抽出では、輪郭が接していてつながったものについては輪郭の面積を用いて異常値として除外した。
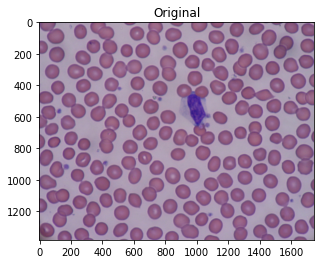 赤血球画像/figcaption>
赤血球画像/figcaption>
2. Watershedを用いた輪郭抽出
赤血球画像を読み込み2値化画像を生成する。2値化画像では、赤血球同士が接しているものは1つの 領域になっている。
orig = cv2.imread(uploaded_file_name)
src = cv2.cvtColor(orig, cv2.COLOR_BGR2RGB)
gray = cv2.cvtColor(orig, cv2.COLOR_BGR2GRAY)
ret, thresh = cv2.threshold(gray,0,255,cv2.THRESH_BINARY_INV+cv2.THRESH_OTSU)
plt.figure(figsize=(4,6))
plt.imshow(thresh,cmap='gray')
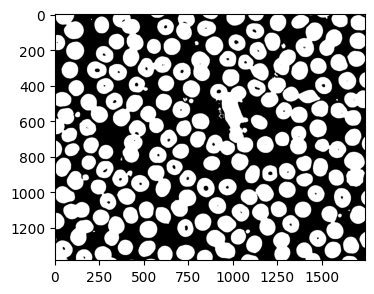 2値化画像
2値化画像
モルフォロジー処理によるノイズや境界除去を行って後、距離変換画像を作成し2値化する。
kernel = np.ones((3,3),np.uint8)
opening = cv2.morphologyEx(thresh,cv2.MORPH_OPEN,kernel, iterations = 2)
sure_bg = cv2.dilate(opening,kernel,iterations=3)
dist_transform = cv2.distanceTransform(opening,cv2.DIST_L2,5)
ret, sure_fg = cv2.threshold(dist_transform,0.7*dist_transform.max(),255,0)
sure_fg = np.uint8(sure_fg)
unknown = cv2.subtract(sure_bg,sure_fg)
plt.figure(figsize=(12,21))
plt.subplot(1,3,1)
plt.imshow(sure_fg,cmap='gray')
plt.subplot(1,3,2)
plt.imshow(dist_transform,cmap='gray')
plt.subplot(1,3,3)
plt.imshow(sure_bg,cmap='gray')
距離変換画像を2値化した画像を前景画像:sure_fgとして、また前景画像と背景画像:sure_bgを不確定領域unknownとする。
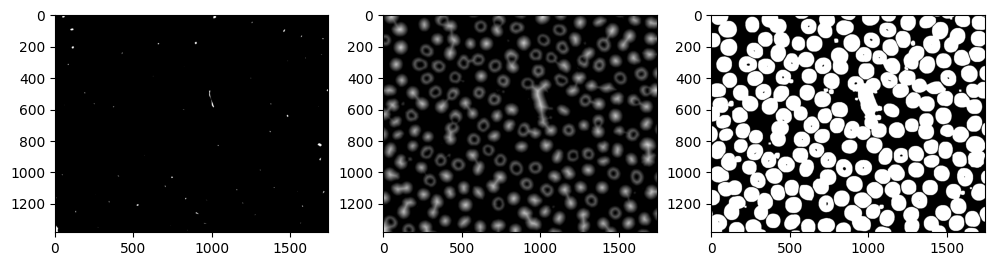 前景、距離、背景
前景、距離、背景
前景画像と不確定領域に基づいてマーカーを作成し、Watershed関数を適用しマーカーを変更する。最後にWatershed関数により変更されたマーカーと元の画像を重ね合わせて抽出された輪郭を確認する。
画像と輪郭の重ね合わせは以下のサイトのコードを利用した。
pystyle.info
ret, markers = cv2.connectedComponents(sure_fg)
markers = markers+1
markers[unknown==255] = 0
src2=src.copy()
markers = cv2.watershed(src2,markers)
labels = np.unique(markers)
blood = []
for label in labels[2:]:
target = np.where(markers == label, 255, 0).astype(np.uint8)
contours, hierarchy = cv2.findContours(
target, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE
)
blood.append(contours[0])
cv2.drawContours(src2, blood, -1, color=(255, 0, 0), thickness=2)
plt.figure(figsize=(5,8))
plt.imshow(src2)
抽出した輪郭を赤線で示した。赤血球が隣接している領域がつながらないように輪郭が抽出できているものがあるが、赤血球同士の重なりが大きいものなどは輪郭がつながっている。また、単体の赤血球の輪郭が抽出できていないものが多い。
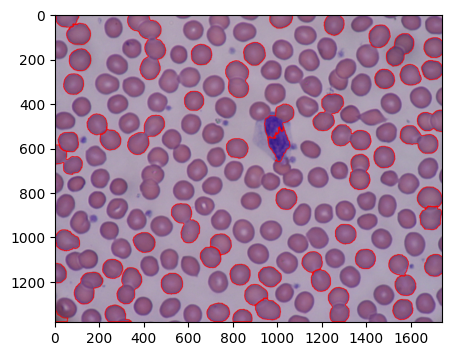 Watershedによる輪郭抽出結果
Watershedによる輪郭抽出結果
3. 距離変換画像の閾値変更
単体の赤血球の輪郭が抽出できていない点は、前景画像生成時に赤血球として抽出できている領域が少ないためで、これを調節するため距離変換画像を2値化する際の閾値を変更してみる。閾値は0.7*dist_transform.max()から0.1*dist_transform.max()の場合の前景画像は以下のように赤血球の領域が、単に2値化した場合と同じぐらいになっている。
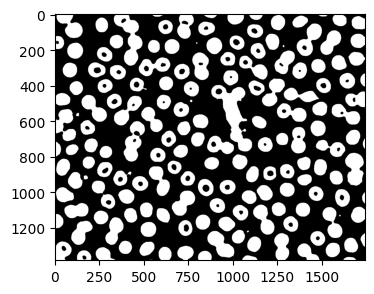 閾値変更後の前景画像
閾値変更後の前景画像
Watershedを適用して輪郭を抽出すると以下のように単体の赤血球は抽出できているが、隣接しているものは領域がつながってしまった。つまり通常の2値化を利用した輪郭抽出と結果が変わらない。
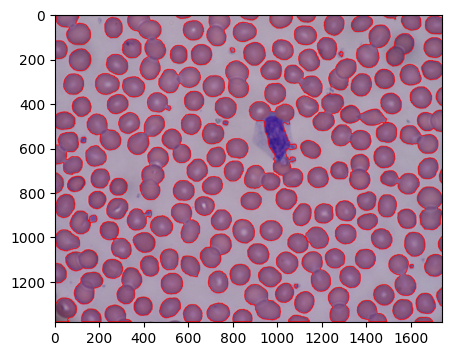 閾値変更後のWatershedによる輪郭抽出結果
閾値変更後のWatershedによる輪郭抽出結果
閾値を小さくすると、領域がつながりやすくなるようなので、閾値を0.5*dist_transform.max()として輪郭抽出すると領域のつながりは減ったが、単体の赤血球の輪郭も減った。
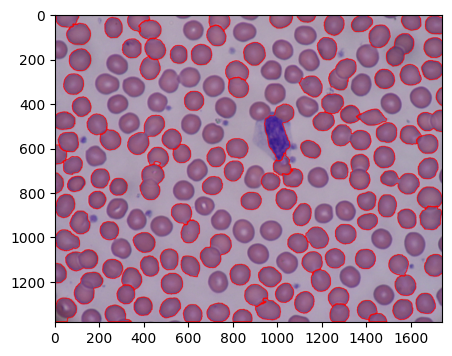 閾値0.5でのWatershedによる輪郭抽出結果
閾値0.5でのWatershedによる輪郭抽出結果
万能な閾値はなさそうなので、閾値が小さい場合と大きい場合を組み合わせて用いるのがよさそうだ。
4. まとめ
今回はWatershedを用いた輪郭抽出の方法と赤血球画像への適用、前景画像作成時の閾値の違いによる輪郭抽出結果の違いについて紹介した。








