Pythonによるデータ処理15 ~ カルマンフィルタ2
前回に引き続いてカルマンフィルタを用いたデータ処理について紹介する。
1. カルマンフィルタモデルのノイズ
カルマンフィルタのモデルとして以下の状態方程式と観測方程式のパラメータについて考える。
Nは正規分布で、Gt, Ft, Wt, Vtは既知(仮定)とした。
今回は状態方程式で仮定しているノイズW, 観測方程式で仮定しているノイズVのカルマンフィルタに対する影響を調べてみる。
2. カルマンフィルタのノイズ値の変更
コード全体は前回記事を参照。
前回はW=1, V=10として観測系のノイズが多いという前提で固定していた。今回はカルマンフィルタ処理の初期値を与えるところの数値を変える。
G = np.array([[1]]) F = np.array([[1]]) W = np.array([[1000]]) # 状態のノイズWを設定 V = np.array([[10000]]) # 観測のノイズVを設定
前回のコード中カルマンフィルタを定義した関数kalman_filterおよびkalman_smoothingの引数を明示的に割り当て、上記の設定した数値が反映されるようにする。
引数を省略していると初回の初期値のみが有効で、初期値の変更が反映されない。
# カルマンフィルター for t in range(T): if t == 0: m[t], C[t] = kalman_filter(m0, C0, data[t:t+1],G,F,W,V) else: m[t], C[t] = kalman_filter(m[t-1:t], C[t-1:t], data[t:t+1],G,F,W,V) # カルマン平滑化 for t in range(T): t = T - t - 1 if t == T - 1: s[t] = m[t] S[t] = C[t] else: s[t], S[t] = kalman_smoothing(s[t+1], S[t+1], m[t], C[t],G,W)
3. ノイズの影響
以下、前回のW=1, V=10の時の元のデータとカルマンフィルタ、カルマン平滑化の効果を示す。W=1,V=10は状態の物理的な外乱(振動とか空気ゆらぎなどの影響で物理的な外乱が加わっている)よりも観測系のセンサ、測定器のノイズが分散で10倍大きいという想定になる。

ここでW,Vの相対関係は崩さず数値を大きくした場合も上記と大きな違いはなく、絶対値の影響は少ないことがわかる。

次にW=1, V=1として状態と観測が同じ程度のノイズとすると、カルマンフィルタは大きな違いはないがカルマン平滑化の滑らかさが減少している。
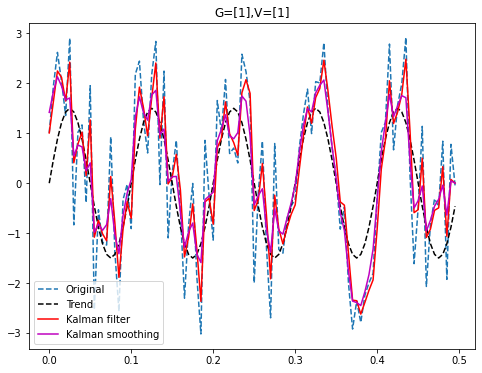
W=1,V=100の場合は、カルマンフィルタ、カルマン平滑化ともにかなり滑らかになっている。これは観測系のノイズが大きいため、元のデータに対してより強いフィルタをかけていることになる。

最後にW=10,V=1として状態のノイズ・外乱が観測のノイズよりも大きいとした場合は、ほとんどフィルタ効果は得られない。

結論としては、初期値としてWよりもVの相対値を大きくすることでカルマンフィルタ、カルマン平滑化のフィルタ効果を調整することができる。