Pythonによるデータ処理8 ～フィルタ処理5

　今回は前回紹介したバタワース、チェビシェフ、楕円特性フィルタを信号データに適用した際の周波数数成分の変化について紹介する。

atatat.hatenablog.com

1. 準備
2. 信号の周波数解析
3. バタワース以外の効果
3. まとめ

1. 準備

設計したフィルタを信号データに適用する方法は以前紹介したが、今回はFFTを用いてフィルタ適用前後の周波数成分がどのように変化するか調べる。

atatat.hatenablog.com

まず、バタワースでバンドパスフィルタを設計して信号データに適用する

import numpy as np
from scipy import signal
from matplotlib import pyplot as plt

samplerate=2500
fp = np.array([499.5,500.5]) # 通過域端周波数[Hz]
fs = np.array([499,501])  # 阻止域端周波数[Hz]
gpass = 3  # 通過域端最大損失[dB]
gstop = 30 # 阻止域端最小損失[dB]
fn = samplerate / 2  #ナイキスト周波数
wp = fp / fn #ナイキスト周波数で通過域端周波数を正規化
ws = fs / fn
N, Wn = signal.buttord(fp, fs, gpass, gstop,True)  #オーダーとバターワースの正規化周波数を計算
b, a = signal.butter(N, Wn, "band",True)  #フィルタ伝達関数の分子と分母を計算
w, h1 = signal.freqs(b, a, np.logspace(1, 3, 100000))

fig, ax1 = plt.subplots()
ax1.set_title('Butterworth response')
ax1.plot(w, 20 * np.log10(abs(h1)), 'b')
ax1.set_ylabel('Amplitude [dB]', color='b')
ax1.set_xlabel('Frequency [rad/sample]')
ax1.set_ylim([-150,10])
ax2 = ax1.twinx()
angles = np.unwrap(np.angle(h1))
ax2.plot(w, angles*180/np.pi, 'g')
ax2.set_ylabel('Angle (Degrees)', color='g')
ax2.grid()
plt.xlim([490,510])

今回は低域側は499.5Hzで通過、499Hzで阻止、高域側は500.5Hzまで通過、501Hzで阻止する狭帯域のバンドパスフィルタとする。阻止域端最小損失は30dBとしたが、これ以上大きくするとフィルタの応答曲線がいびつになる。バタワースバンドフィルタの応答は以下のようになる。

信号データはサンプリングレート2500で10秒間のガウシアンランダムノイズを使用する。

x = np.arange(0, 25000) / samplerate   
data = np.random.normal(loc=0, scale=1, size=len(x))    # ガウシアンノイズを生成
plt.figure(figsize=(5,3))
plt.plot(x,data)

フィルタ実行する関数を定義して、上記のdataに適用する。注意点としては、signal.buttordとsignal.butterのアナログオプションをデフォルトのFalse (オプションを指定しない)に戻しておく必要がある。

#バターワースフィルタ
def bandpass(x, samplerate, fp, fs, gpass, gstop):
    fn = samplerate / 2    #ナイキスト周波数
    wp = fp / fn   #ナイキスト周波数で通過域端周波数を正規化
    ws = fs / fn    #ナイキスト周波数で阻止域端周波数を正規化
    N, Wn = signal.buttord(wp, ws, gpass, gstop)  #オーダーとバターワースの正規化周波数を計算
    b, a = signal.butter(N, Wn, "band")  #フィルタ伝達関数の分子と分母を計算
    y = signal.filtfilt(b, a, x)   #信号に対してフィルタをかける
    return y  

# フィルタ関数を実行
data_bandfilt = bandpass(data, samplerate, fp, fs, gpass, gstop)

2. 信号の周波数解析

　次にdataとフィルタを適用したdata_bandfiltの周波数成分を調べる。fft関数はいろいろなモジュールで提供されているが、今回はNumpyのfftモジュールを使用する。以下のようにnp.fft.fft(data)とするとfftamp0は複素数で数値が返ってくるので、例えば絶対値をとってさらにlogに20をかけることで相対的なdB表示することができる。（正確にはリファレンスになる電圧やパワーレベルで割っておく必要があるので、ここで使っているdBの絶対値は正しくない）周波数軸は10秒間のデータなので周波数増分は1/10=0.1Hzとなり、サンプリングレートは2500なので0から0.1Hzずつ2500Hzまでがフルスケールになるが、ナイキスト定理により1250Hzまでが有用な周波数範囲となる。

fftamp0=np.fft.fft(data)
fftamp1=np.fft.fft(data_bandfilt)
df=0.1
fx=np.arange(0,2500,0.1)
np.size(fx)
plt.plot(fx,20*np.log10(np.abs(fftamp0)))
plt.plot(fx,20*np.log10(np.abs(fftamp1)))
plt.xlim([497,503])
plt.vlines(499.5,-40,60,'green','dashed')
plt.vlines(500.5,-40,60,'green','dashed')
plt.xlim([495,505])
plt.ylim([-40,60])
plt.legend(['Raw','Butterworth band'])

縦の緑破線は通過周波数端の499.5Hzと500.5Hzを示している。バンドパスフィルタ適用後の信号データは通過帯域以外は減衰していることがわかる。

3. バタワース以外の効果

　上のバタワースフィルタと同じ手順で第１種チェビシェフ、第２種チェビシェフ、楕円フィルタでバンドパスフィルタを設計して信号データに適用する。通過、阻止帯域はバタワースと同じだが、阻止域最小損失を各フィルタで特性がひずまないよう程度の値まで大きくしている。以下のコードはバタワースからの主な変更のみを示し、fftやプロットの部分はほぼ胸中なので省略する。

#第１種チェビシェフフィルタ
def bandpass_ch1(x, samplerate, fp, fs, gpass, gstop):
    fn = samplerate / 2   
    wp = fp / fn   
    ws = fs / fn   
    N, Wn = signal.cheb1ord(wp, ws, gpass, gstop)  
    b, a = signal.cheby1(N,3, Wn, "band")  
    y = signal.filtfilt(b, a, x)  
    return y  

fp = np.array([499.5,500.5]) # 通過域端周波数[Hz]
fs = np.array([499,501])  # 阻止域端周波数[Hz]
gpass = 3  # 通過域端最大損失[dB]
gstop = 35 # 阻止域端最小損失[dB]

data_bandfilt = bandpass_ch1(data, samplerate, fp, fs, gpass, gstop)

"第１種チェビシェフバンドパスフィルタ" — 第１種チェビシェフバンドパスフィルタ

第１種チェビシェフフィルタは通過帯域のリップルを許容するため、信号データの周波数成分に対して差が生じている。

"第１種チェビシェフバンドパスの周波数変動" — 第１種チェビシェフバンドパスの周波数変動

#第２種チェビシェフフィルタ
def bandpass_ch2(x, samplerate, fp, fs, gpass, gstop):
    fn = samplerate / 2  
    wp = fp / fn 
    ws = fs / fn 
    N, Wn = signal.cheb2ord(wp, ws, gpass, gstop)  
    b, a = signal.cheby2(N,gstop, Wn, "band")  
    y = signal.filtfilt(b, a, x)  
    return y  
fp = np.array([499.5,500.5]) # 通過域端周波数[Hz]
fs = np.array([499,501])  # 阻止域端周波数[Hz]
gpass = 3  # 通過域端最大損失[dB]
gstop = 35 # 阻止域端最小損失[dB]

data_bandfilt = bandpass_ch2(data, samplerate, fp, fs, gpass, gstop)

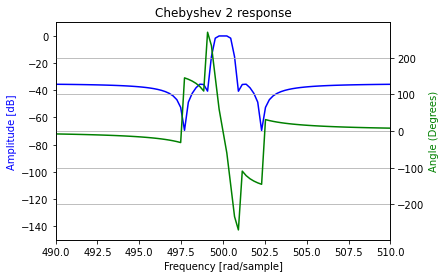
"第２種チェビシェフバンドパスフィルタ" — 第２種チェビシェフバンドパスフィルタ

第２種チェビシェフフィルタは通過帯域のリップルはないため、信号データの周波数成分は第１種チェビシェフフィルタよりも一致している。

"第２種チェビシェフバンドパスの周波数変動" — 第２種チェビシェフバンドパスの周波数変動

#楕円フィルタ
def bandpass_ell(x, samplerate, fp, fs, gpass, gstop):
    fn = samplerate / 2  
    wp = fp / fn 
    ws = fs / fn  
    N, Wn = signal.ellipord(wp, ws, gpass, gstop) 
    b, a = signal.ellip(N,3,gstop, Wn, "band") 
    y = signal.filtfilt(b, a, x) 
    return y  
fp = np.array([499.5,500.5]) # 通過域端周波数[Hz]
fs = np.array([499,501])  # 阻止域端周波数[Hz]
gpass = 3  # 通過域端最大損失[dB]
gstop = 55 # 阻止域端最小損失[dB]

data_bandfilt = bandpass_ell(data, samplerate, fp, fs, gpass, gstop)