Pythonによるデータ処理7 ～フィルタ処理4

　前回まではバタワース特性に基づいたフィルタを紹介したが、今回はバタワース特性以外のチェビシェフ、楕円特性に基づいたフィルタについて紹介する。

atatat.hatenablog.com

1. フィルタ周波数特性
2. バタワースフィルタ周波数特性
3. チェビシェフフィルタ周波数特性
4. 楕円フィルタの周波数特性と比較
5. まとめ

1. フィルタ周波数特性

バタワースフィルタの周波数応答は通過帯域では最大限平坦であり（リップルがない）、除去帯域に向かってゼロに近づくという特徴がある。ただし、逆にカットオフ周波数での遮蔽特性がなだらかになるという欠点があり、より急峻な遮蔽特性をもつフィルタとしてチェビシェフフィルタ、楕円フィルタが知られている。今回は急峻な遮蔽特性をもつチェビシェフフィルタ(1種、2種)、楕円フィルタと位相遅れが平坦なベッセルフィルタについて紹介する。なおScipyで利用できるフィルタと使用方法は

docs.scipy.org

Matlab-style IIR filter designに記されている。

2. バタワースフィルタ周波数特性

　まず通過帯域端500Hz、阻止帯域端510Hzで阻止帯域端10dBのバタワースローパスフィルタを以下のように設計して、特性を表示する。阻止帯域端10dB以上にすると解が得られない。

import numpy as np
from scipy import signal
from matplotlib import pyplot as plt

#周波数特性の設定
samplerate = 25600
fp = 500  #通過域端周波数[Hz]
fs = 510 # 阻止域端周波数[Hz]
gpass = 3  # 通過域端最大損失[dB]
gstop = 10 # 阻止域端最小損失[dB]
fn = samplerate / 2  #ナイキスト周波数


#フィルタ特性計算 (バタワース)
N, Wn = signal.buttord(fp, fs, gpass, gstop,True)  #オーダーと正規化周波数を計算
b, a = signal.butter(N, Wn, "low",True)  #フィルタ伝達関数の分子と分母を計算
w, h1 = signal.freqs(b, a, np.logspace(1, 3, 100))

#プロット
fig, ax1 = plt.subplots()
ax1.set_title('Butterworth response')
ax1.plot(w, 20 * np.log10(abs(h1)), 'b')
ax1.set_ylabel('Amplitude [dB]', color='b')
ax1.set_xlabel('Frequency [rad/sample]')
ax2 = ax1.twinx()
angles = np.unwrap(np.angle(h1))
ax2.plot(w, angles*180/np.pi, 'g')
ax2.set_ylabel('Angle (Degrees)', color='g')
ax2.grid()

3. チェビシェフフィルタ周波数特性

次に第一種チェビシェフフィルタを設計するにはバタワースとほぼ同様の手順で通過域端周波数、阻止域端周波数、通過域端最大損失、阻止域端最小損失を指定して次数Nと正規化周波数Wnを算出し、N,Wnからフィルタ係数b,aを算出する。第一種チェビシェフフィルタの場合は N, Wn = signal.cheb1ord(fp, fs, gpass, gstop,True)とb, a = signal.cheby1(N,3, Wn, "low",True)を用いる。signal.cheby1()の2番目の引き数3は通過帯域の許容リップル(dB)を指定する。チェビシェフフィルタは急峻な遮蔽特性をもつことを利用して阻止域端最小損失を50dBで設計した。以下バタワースと異なる部分のコードを記す。

#フィルタ特性計算 (第一種チェビシェフ)
gpass = 3  # 通過域端最大損失[dB]
gstop = 50 # 阻止域端最小損失[dB]
N, Wn = signal.cheb1ord(fp, fs, gpass, gstop,True)  #オーダーと正規化周波数を計算
b, a = signal.cheby1(N,3, Wn, "low",True)  #フィルタ伝達関数の分子と分母を計算
w, h2 = signal.freqs(b, a, np.logspace(1, 3, 100))

得られた第一種チェビシェフフィルタの周波数特性を以下に示すが、通過帯域のリップルを許容する代わりにカットオフ周波数での急峻な遮蔽特性を実現している。

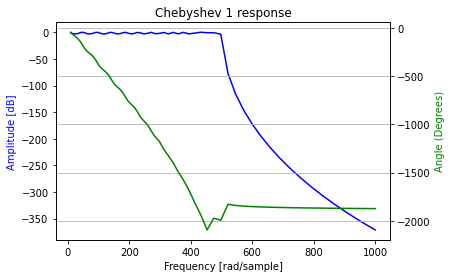
第二種チェビシェフフィルタの場合は N, Wn = signal.cheb2ord(fp, fs, gpass, gstop,True)とb, a = signal.cheby2(N,gstop, Wn, "low",True)を用いる。signal.cheby2()の2番目の引き数は遮蔽後の最低減衰量で指定したdB値以下で振幅特性が変動する。バタワースや第一種チェビシェフフィルタは周波数が上がるにつれて減衰が大きくなるが、第二種チェビシェフフィルタの場合はそうではない。今回は阻止域端最小損失50dBをそのまま使用した。

#フィルタ特性計算 (第二種チェビシェフ)
gpass = 3  # 通過域端最大損失[dB]
gstop = 50 # 阻止域端最小損失[dB]
N, Wn = signal.cheb2ord(fp, fs, gpass, gstop,True)  #オーダーと正規化周波数を計算
b, a = signal.cheby2(N,gstop, Wn, "low",True)  #フィルタ伝達関数の分子と分母を計算
w, h3 = signal.freqs(b, a, np.logspace(1, 3, 100))

第一種チェビシェフフィルタと違って通過帯域ではリップルはなく平坦になっていることが特徴。

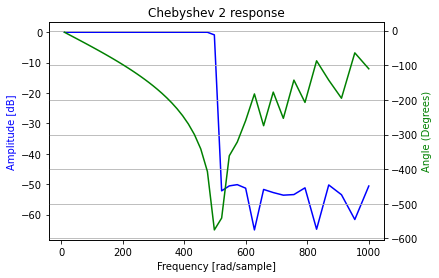
4. 楕円フィルタの周波数特性と比較

最後の楕円フィルタは通過帯域、遮蔽後の両方でリップルを許容する代わりに、チェビシェフフィルタよりも急峻な遮蔽特性が得られる。次数と正規化周波数はN, Wn = signal.ellipord(fp, fs, gpass, gstop,True)を用いて、フィルタ係数はb, a = signal.ellip(N, 3, gstop, Wn, "low",True)で得られる。signal.ellip()の2番目は通過帯域で許容できるリップルで3dBを指定、3番目は遮蔽後の最低減衰量でgstopを使用した。チェビシェフフィルタよりも阻止域端最小損失を大きくすることができ、100dBを指定した。

#フィルタ特性計算 (楕円)
gpass = 3  # 通過域端最大損失[dB]
gstop = 100 # 阻止域端最小損失[dB]

N, Wn = signal.ellipord(fp, fs, gpass, gstop,True)  #オーダーと正規化周波数を計算
b, a = signal.ellip(N, 3, gstop, Wn, "low",True)  #フィルタ伝達関数の分子と分母を計算
w, h4 = signal.freqs(b, a, np.logspace(1, 3, 100))

最後に、通過域端周波数, 阻止域端周波数を500,510Hzとしたローパスフィルタでバタワース、第一種チェビシェフ、第二種チェビシェフ、楕円フィルタでの振幅周波数特性を比較した。

plt.plot(w, 20 * np.log10(abs(h1)), 'r')
plt.plot(w, 20 * np.log10(abs(h2)), 'g')
plt.plot(w, 20 * np.log10(abs(h3)), 'b')
plt.plot(w, 20 * np.log10(abs(h4)), 'm')
plt.legend(['Butterworth','Cheby1','Cheby2','Elliptic'])
plt.title('Amplitude response')
plt.xlabel('Frequency [rad/sample]')
plt.ylabel('Amplitude [dB]')
plt.ylim([-100,10])
plt.grid()