gnuplotによるグラフ作成28~組み込み特殊関数のプロット
今回はgnuplotでの特殊関数のプロットについて紹介する。組み込みで使用できる関数は、メニューバーのFunctionsでElementaryが基本関数、Specialが特殊関数、Statisticalは統計関数で確認できるが、一般的な数値計算ソフト等に対しては種類が少ないので、組み込みで使用できないものは自分で関数を定義する必要がある。
1. 統計関数
統計関数は累積正規分布を返すnorm(x)とその逆関数のinvnorm(x)が使用できる。
plot norm(x)

set xrange[0:1] plot invnorm(x)

2. 特殊関数
誤差関数はerf(x)で相補誤差関数(1-erf(x))はerfc(x)
set xrange[-10:10] plot erf(x),erfc(x)

誤差関数の逆関数はinverf(x)
set xrange[-1:1] plot inverf(x)

ガンマ関数はgamma(x)
set xrange[0:5] plot gamma(x)
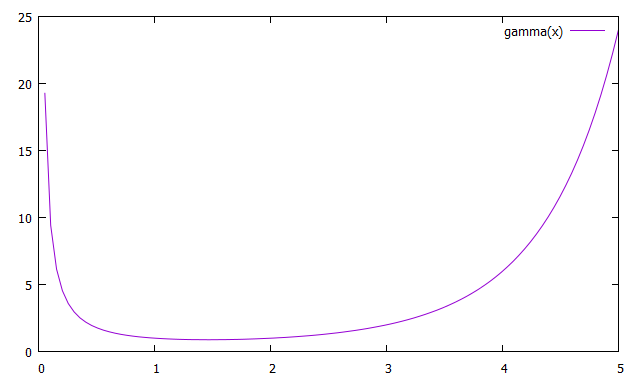
xの引数が大きい場合はlgamma(x)を用いるとガンマ関数の値の自然対数をとった値を返す。
不完全ガンマ関数(定義は不完全ガンマ関数 - 高精度計算サイトなど参照)は
plot igamma(1,x)

不完全ベータ関数(定義は不完全ベータ関数 - 高精度計算サイトなど参照)は
set xrange[0:1] plot ibeta(1,3,x)

第1種の0次ベッセル関数はbesj0(x)、1次ベッセル関数はbesj1(x)、第2種の0次ベッセル関数はbesy0(x)、1次ベッセル関数はbesy1(x)をそれぞれ用いる。
set xrange[0:10] set yrange[-1:1] plot besj0(x),besj1(x),besy0(x),besy1(x)

ランベルトのW関数の主値(定義はwikipedia:ランベルトのW関数など参照)は
set trange[0:2] plot lambertw(x)

3. まとめ
よく使う特殊関数は組み込み関数になっているが、統計関連の関数は正規分布のみの最低限しか組み込み関数になっておらず、gnuplotを使う場合は関数を定義する必要がある。